【解答編】数学の知識一切不要の、超難解な天秤の問題をあなたは解けますか？
31 コメント
難解な天秤の問題の解答例をご紹介します。
パイナポー
シナモン
ジャガアポー
ガチで便利！Mac歴100年の僕が最強だと思う、US配列キーボードの日本語入力環境設定
【Windows編】僕がブログ更新時に使う8つのアプリ
Moxbitの更新再開と次期バージョンについて
マウスカーソルと棒人間が戦うFlashアニメ『Animator vs. Animation』が面白い
『Moxbit 4.5 GoldenEagle』へアップデート
この記事への最近のコメント
ゲゲゲのゲスト
きゅーさんの言っていた14このおもりの場合はより数学的にとくことができて好きですね。まず3こで重いか軽いかわかるおもりまたは重いか軽いかわからないが重さが違う2...
m
6・6・1でもできるのか？と思ったのですが、いかがでしょうか。
左からABCとすると、
①ABを比べる→ABが釣り合ったらCが軽い
→ABで傾けば...
匿名
ありがとうございます...
べつ
自分は4、4、5の分け方の別のやり方で解けました！...
ゲゲゲのゲスト
どうやるんですか？...
- この記事の目次
重いか軽いかわからない天秤の問題
先週ご紹介した天秤の問題、あなたは分かりましたか？
13個の“おもり”がある。この中に1つだけ重さの違うおもりがある。
天秤（てんびん）を3回だけ使い、重さの違うおもりを判別する方法を答えよ。
ただし、重さの違うおもりは重いのか軽いのか分からない。
この問題の一番の特徴は“重さの違うおもりは、軽いか重いか分からない”ところです。
シナモン
それでは早速解答編のスタートです。
おもりの分け方
こういった天秤を使って違う重さのおもりを判断する問題は、どのような分け方でおもりをグループ化するかが重要になります。
今回の問題の場合は、4・4・5でわけます。重さの違うおもりが重いか軽いかわかっている場合は、いろいろなおもりの分け方がありましたが、今回の問題はおそらく 4・4・5 以外の分け方では解けないかと思います。
シナモン
パイナポー
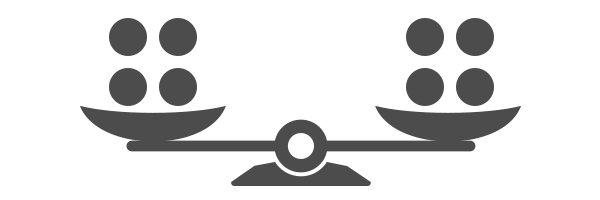
そして5つのおもりは置いておき、残りの4・4を天秤にかけます。この時点で、天秤を使えるのは残り2回となります。
4・4を天秤にかけて、つりあった場合
4・4を天秤にかけてつりあった場合、片方の4つのおもりともう片方の4つのおもりの重さは全く同じです。この問題では、重さのちがうおもりは1つしか入っていないため、この時点でこれら8つの中には重さのちがうおもりは入っていないことになります。そのためこれら8つのおもりは、基準となる重さをもつおもりとなります。
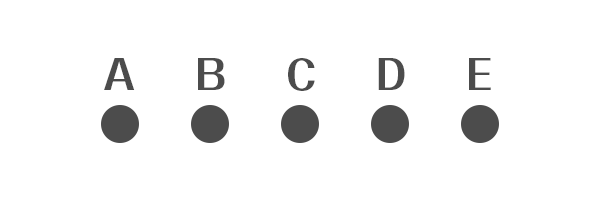
したがって求めているおもりは、5つの中にあることが分かりました。分かりやすくなるように、これらに記号を振っておきます。また今後、画像内の青いおもりは基準となる8つのおもりを表しています。
これらA〜Eの5つのうち3つを取り出して、基準となるおもりと天秤にかけます。画像ではABCと、基準となるおもりを天秤にかけています。この時点で天秤を使えるのは残り1回。
もしこの状態でABCと基準となるおもり3つがつりあっていれば、答えはDかEの中にあります。Dと基準となるおもり1つを天秤にかけ、天秤がつりあった場合は、Eが答えとなります。つりあわなかった場合は、Dが答えとなります。
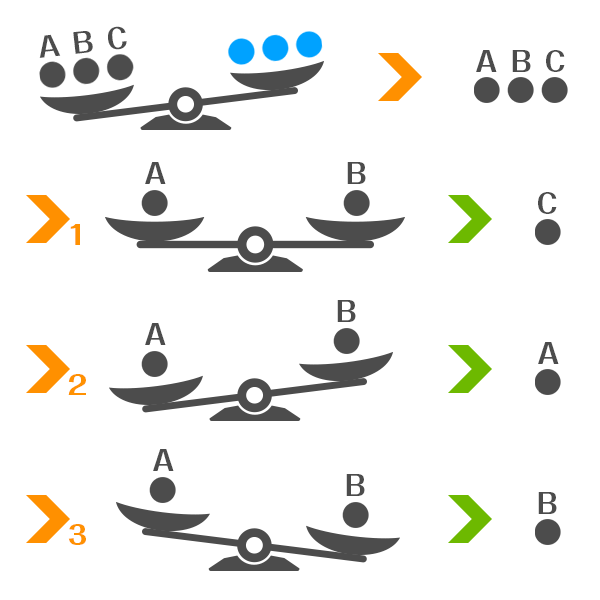
次にABCと基準となるおもりがつりあわなかった場合、残りのDEの中には答えがないこととなり、ABCの中に答えがあることが分かります。ここで重要なのは、「ABCと基準となるおもり3つを天秤にかけたとき、どちらに傾いたか」です。このとき、
- ABCの皿が下がった場合、重さの違うおもりは“重い”
- ABCの皿が上がった場合、重さの違うおもりは“軽い”
ことが分かります。まずはABCの皿が下がったことを前提として話を進めます。ちなみに天秤を使える回数は残り1回です。
これらABCの中から2つ選び、天秤にかけます。ABをかけてつりあった場合、Cが答えになります。ABCの皿が下がったということは、重さの違うおもりは“重い”ことがわかっているため、ABをかけてつりあわなかった場合、皿が下がった方が答えのおもりとなります。
ABCと基準となるおもり3つを天秤にかけたとき、ABCの皿が上がった場合はこの逆となります。すなわち重さの違うおもりは“軽い”ことがわかっているため、ABを天秤にかけて皿が上がった方が、答えのおもりとなります。
これで最初に4・4・5にわけ、4・4がつりあった場合の重さの違うおもりを見つける方法を証明できました。
4・4を天秤にかけ、つりあわなかった場合
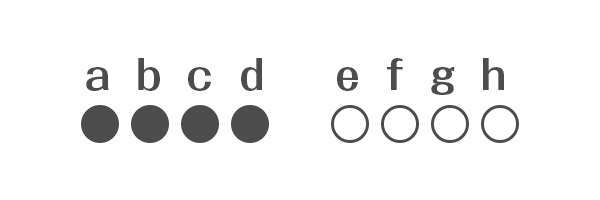
分かりやすくなるように、それぞれに記号を振っておきます。4・4にわけたうちの片方をa〜d、もう片方をe〜hとします。
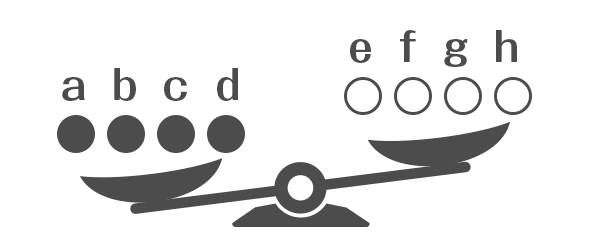
4・4を天秤にかけてつりあわなかった場合、残りの5つのおもりには重さの違うおもりが入っていないことになります。したがって、この時点でこれら8つの中に答えがあることになります。
ここで、この4・4を天秤にかけたとき、どちらに皿が下がったかが重要となりますので覚えておいてください。ちなみにこの時点で天秤を使える回数は残り2回です。
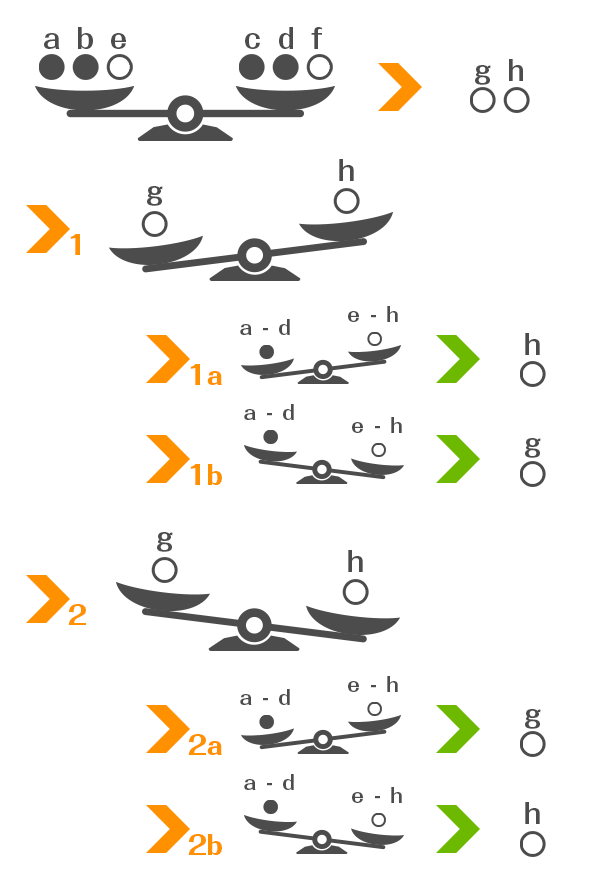
“abcdの中から2つ、efghから1つ”を1セットとし、これを2セット分取り出して天秤にかけます。画像ではabe、cdfといった組み合わせで天秤にかけています。
この時点でつりあったのであれば、天秤にかけていないgかhのどちらかが答えのおもりとなります。すなわち、abcdは基準となる重さをもつおもりとして扱えます。天秤を使えるのは残り1回です。
次にあまった2つのおもり、gとhを天秤にかけます。このとき、1回目のabcdとefghを天秤にかけたとき、どちらの皿が下がったかで答えのおもりが分かります。
gとhを天秤にかけて、gの皿が下がったときの場合を見てましょう。1回目でabcdの皿がさがっているならば、hが答えとなります。このhは通常より“軽い”重さをもつおもりとなります。1回目でabcdの皿があがっているならば、gが答えとなります。このgは通常より“重い”重さをもつおもりとなります。
次にgとhの天秤で、gの皿が上がったときの場合です。1回目でabcdの皿がさがっているならば、gが答えとなります。このgは通常より“軽い”重さをもつおもりとなります。1回目でabcdの皿があがっているならば、hが答えとなります。このhは通常より“軽い”重さをもつおもりとなります。
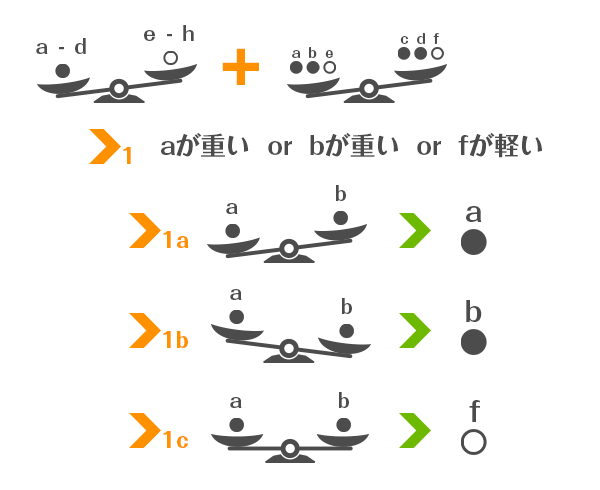
次に、abc、cdfの組み合わせで天秤にかけたとき、つりあわなかった場合を考えてみます。ちなみに天秤を使えるのはあと1回までです。
1回目でabcdの皿がさがり、そして先ほどの2回目でabeの皿が下がった場合、答えのおもりは3つにしぼることができます。
それは
- aが答えで、通常より“重い”おもり
- bが答えで、通常より“重い”おもり
- fが答えで、通常より“軽い”おもり
です。
ここでaとbを天秤にかけます。このときaの皿が下がったら、aが答えになります。このときbの皿が下がったら、bが答えになります。このときaとbがつりあったら、fが答えになります。
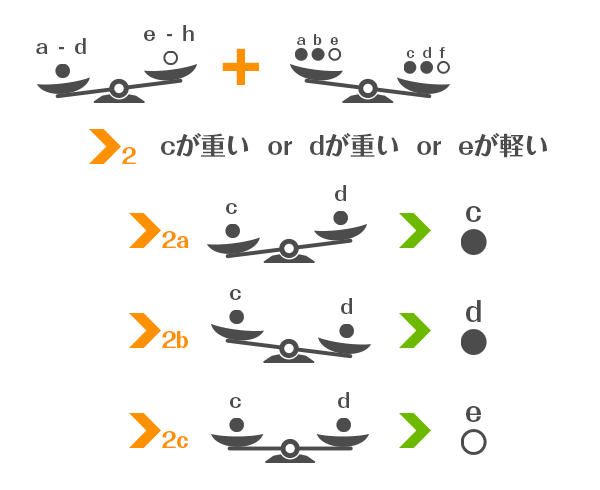
次に1回目でabcdの皿がさがり、2回目でcdfの皿が下がる、すなわちabeの皿が上がった場合を考えます。このとき答えは
- cが答えで、通常より“重い”おもり
- dが答えで、通常より“重い”おもり
- eが答えで、通常より“軽い”おもり
の3つにしぼることができます。
ここでcとdを天秤にかけ、このときcの皿が下がったら、cが答えになります。このときdの皿が下がったら、dが答えになります。このときcとdがつりあったら、eが答えになります。
1回目の皿が上がった場合は、3回目の結果の逆となり、同様にして求められます。
これで4・4がつりあわなかったときの答えも求められ、本問題においてのすべての答えを導出するパターンを証明できました。
この記事で紹介したモノ
- -
あとがき
パイナポー
シナモン
ジャガアポー
パイナポー
シナモン
パイナポー
ジャガアポー
シナモン
ジャガアポー
パイナポー
ジャガアポー
パイナポー
シナモン
記事は執筆時の情報に基づいており、現在では異なる場合があります。
この記事をシェアする
＼(^o^;)／
1回目で、4-4がつり合ったときの証明を忘れておりました･･･
別回答を見つけたのでご報告します。間違ってたらすみません。
1.おもりを3.3.3.3.1と分ける
(それぞれA.B.C.D.Eとする)
2.AとBを天秤にかける
3.CとDも天秤にかける
この時点で両方とも釣り合った場合は答えはEのおもりになる
釣り合わなければ、ひとつだけ重さの違うグループができるはずなので、そのグループを特定する。また、このとき、そのグループが他のグループに対して重かったか軽かったか覚えておく(*)。
その3つの重りを2つ取り出して、天秤にかける。釣り合わなければ、(*)のときに重かったなら重いおもり、軽かったなら軽いおもりが答え。釣り合えば、残りのひとつが答え。
どうでしょうか？
横からすいません、質問です～
たとえばAとBでAが重く、CとDがつり合ったとき、重さの違うおもりがAかBのどちらに入っているかはどうやって判断するのですか？
oh...
そんなところが間違っていましたか・・・盲点でした。
結構自信あったんだけどなー。間違えてすいません。
難しかったですよね(^-^;
俺も「分かった＼(^o^)／」とか言って分かってなかったクチですしw
4•4がを天秤にかけて、つりあった場合しかよくわからないです。。。
基準を使うのはいいのですが3つ使うことに思い至らなかったー
おもしろかったです！
みなさん苦戦していますね〜。といっても、僕も解けなかった身なんですがね（汗）
重いか軽いか分かっている場合はパターンが重要になりますが、わからない場合は考え方が重要になりますね。
4,4で釣り合わなかった場合は、余った5個とabcefを比べてもできそうですね。
二回目の天秤でabcef側が下がったらabcのどれかが重くて、上がったらefのどちらかが軽い。
釣り合ったらdghが怪しい、つまり、dが軽いか、ghの一方が重いということになります。
お〜！
たしかにその方法でもできますね、素晴らしい！この記事で紹介した方法より理解しやすい解法かもしれません。
I can 説破！面白いですね！
でしょでしょー！
13個のおもりの問題の解答で最初らへんのEが答えとなりますってありますけど、重いか軽いかわかります？
基準（通常の重さのおもり）と比較しているので、その傾きで重いか軽いかが分かります。基準の方が上がったら、異なる重さのおもりは重い、基準の方が下がったら、異なる重さのおもりは軽い、ということになります。
Eは天秤にかけないから分からないじゃないんじゃないですか？
4.4でつりあってabcと基準のおもりがつりあってdと基準のおもりを比べた時です
おぉっと…、確かに重いか軽いかは分かりませんね…これはこれは失礼しました；
Dと基準が釣り合ったら、重さの違うおもりはEとなりますが、そのEが軽いか重いかは分かりません。ただしDと基準が釣り合わなかった場合、前の僕のコメントのように、天秤の傾きでDが軽いか重いかは分かります。
分かりました、ありがとうございます。
この問題は「重いか軽いかまで必ず判別しなければならない」とすると、理論上、絶対に解けません。
ケンさんが指摘している通り、記事の方法は「3回とも釣り合った場合、Eが重いか軽いか分からない」わけですが、これが許されるから解けるわけです。
以下証明。
おもりは13個あるので、正解候補は「おもり1が重い」「おもり1が軽い」「おもり2が重い」…「おもり13が軽い」の26通りです。
一方、3回天秤を使うと、それぞれで「右が重い」「左が重い」「釣り合う」の3通りの可能性があるので、全部で3×3×3＝27通りの可能性があります。
これだけ見れば、比べるおもりをうまく選べば重いか軽いかまで判別できそうな気がします。
ところが、初手で4個と4個を比べると、釣り合わなかったら正解候補を8通りに絞れますが、釣り合ったら10通りの正解候補が残ってしまいます。
天秤を2回使うと9通りの可能性があるので、8通りの正解候補の中から1つの正解に絞ることは可能ですが、10通りの正解候補の中から1つに絞ることはどうあがいても不可能です。
同様に、初手で3個と3個を比べると、釣り合った時に14通りの正解候補が残ってしまい、初手で5個と5個を比べると、釣り合わなかった時に10通りの正解候補が残ってしまいます。
1個、2個、6個でも同様。
以上で、「重いか軽いかまで必ず判別しなければならない」とすると、この問題は絶対に解けないことが証明できました。
実際にはこの問題は、重いか軽いかまでは判別しなくてもいいわけですが、「重いか軽いかは分からないけど、この1個の重さが違うことだけは分かる」という状況は、「3回とも釣り合って、3回とも天秤に乗せなかったおもりが1個だけある」という状況以外にあり得ません。
すなわち、最初の1手で釣り合わなかった場合は正解候補は9通り以下に絞らなくてはならないし、釣り合った場合でも正解候補が11通り以上あってはいけないわけです。
以上で、最初の1手は「4個と4個を比べる」以外にあり得ないことが証明できました。
超遅レスで失礼しました。
余談ですが、問題をちょっと弄って次のようにすると、重いか軽いかまで判別できるようになります。
14個の“おもり”がある。この中に1つだけ重さの違うおもりがある。
14個のうち1個は、他と重さが違うおもりではないことが分かっている。
天秤を3回だけ使い、重さの違うおもりがどれか、それが重いか軽いか判別する方法を答えよ。
ジャガアポーさんなら解けますよね。
ぐへ〜〜、頭疲れそうです＠＠
はじめまして。今日このサイトを見つけました。「このサイトは頭のいい人が作ってそう」な雰囲気で、感じが良くて、少し読ませてもらいました（カメラの記事や万年筆の記事や温泉街の記事など）
この問題ですが、最初、ジャガアポーさんが考えたのだと思って、やっぱ頭のいい人だったんだ！と、一人で納得してました（笑）。だって「寄稿した」って書いてあるし。
私の回答は、こちらの解答とは別パターンでした。こちらの回答はかなりハイレベルで、思いつきませんでした。
この問題、面白いですね。「天秤を三回しか使えない」状況って何だ～と考えると、ちょっと笑えます。（面白いってそっちかっ（笑）。いえいえ、パズル問題として大変面白いです）
＞これらA〜Bの5つのうち3つを取り出して
あと、これ↑は誤植でしょうか。
残念ながら僕が作った問題ではありません（汗）
僕自信もどこで知ったのか覚えていないのです…。
この手の問題は「どんなシチュエーションだよ！」と思うことが多いですよね（笑）
ま、それはご愛嬌ということで…！
誤植の部分、修正しました。ご報告ありがとうございます！
例えば次の様にすれば、はかり方は固定でも判定できます。
重りを A,B,...,M とします。
重さが他と異なる重りを X とよびます。
次のように天秤を使います。
1回目 B,E,H,I と C,D,F,G を比べる。
2回目 B,G,J,L と C,H,I,K を比べる。
3回目 C,F,J,M と D,G,I,L を比べる。
これらの結果からXがA以外の場合はXの正体とその軽重が分かります。
例えば
B,E,H,I が C,D,F,G より重く、
B,G,J,L が C,H,I,K より軽く、
C,F,J,M が D,G,I,L と釣りあう場合、
XはHで重いと分かります。
これは例えば次のように確かめられます。
３回目だけ釣りあったので、Xは１回目と２回目は天秤にのっており、３回目はのっていない。
よってXはBかH。
Bは軽ければ１回目の比較結果に矛盾し、重ければ２回目の比較結果に矛盾するのでXではありえない。
XがHで重いとすると比較結果に矛盾しない。
XがAの場合、３回とも釣り合うのでXがAであることは分かりますが、重いか軽いかはわかりません。
既に他の人が指摘しているように天秤を３回使ってXの正体と軽重を両方必ず判定するのは不可能です。
比較結果から答えを求めるのが面倒だと思われるかもしれませんが、ありうる２５通り（３回とも同じ方に傾くパターン２通りは起こらない）の比較結果に対して答えを前もって求めておくことはできます。
要するに最初にひと手間かけて答えの表を用意すれば以降はいろいろ場合分けをせずとも毎回同じ操作＋表引きで答えが求まります。
5個5個3個だってできるよ。3回以内なら。やってみて
どうやるんですか？
自分は4、4、5の分け方の別のやり方で解けました！
ありがとうございます
6・6・1でもできるのか？と思ったのですが、いかがでしょうか。
左からABCとすると、
①ABを比べる→ABが釣り合ったらCが軽い
→ABで傾けば、そのうちの軽い方を3・3に分け、DEとする
②DEを比べる→DEで傾けば、そのうちの軽い方を1・1・1でFGHとする
③FGを比べる→FGで傾けば、軽い方が正解
→FGで釣り合ったらHが正解
きゅーさんの言っていた14このおもりの場合はより数学的にとくことができて好きですね。まず3こで重いか軽いかわかるおもりまたは重いか軽いかわからないが重さが違う2このおもりは1回で特定できますからそれに帰着出来るようにおもりを調整しますまず8と6に分けて8を4と4で天秤にかけ釣り合った場合3と3では最初のやつに帰着できないので6を2と2と2に分けて天秤にかければ最初に述べた2このおもりがもとまります釣り合わなければ最初の形に帰着するために2と3と3に分ければいいと想像できますそこで両方から1っこづつ引き釣り合った場合残りの2こが最初に述べた形となり釣り合わなかった場合3っつが重いか軽いか特定すればいいから本物の6つのコインと釣り合わなかった6つのコインを天秤にかければ偽物のコインが重いか軽いかを特定でき釣り合わなかった3つのコインのくみから条件を満たす方を選べば最初に帰着でき終わりです